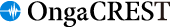統計的機械学習に基づく音楽解析

吉井 和佳, 持橋 大地*1, 後藤 真孝*2

京都大学, *1統計数理研究所, *2産業技術総合研究所

音楽データの教師なし構造学習を目指して

確率的な枠組みを用いて類似度・ありがち度の計算に客観的な裏付け (エビデンス) を与えたい

  • 類似度・ありがち度：ある確率モデル (個別楽曲モデル・全楽曲モデル) から与えられた音楽データが生成される確率
  • 確率が大きい＝予測しやすい → 確率モデルの学習に用いたデータに対して類似度・ありがち度が大きい

WEB上に存在する大量の音楽データから音楽に内在する構造を教師なしで学習したい

  • 音楽データ (信号・記号データ) の生成過程を、理論上は「無限の複雑さ」 をもつノンパラメトリックベイズモデルで表現
  • 実際には有限の音楽データが与えられると、それを説明するのに必要な「実効的な複雑さ」が自動的に決定 → 構造学習が可能

p28_top

音楽音響信号に対するノンパラメトリックベイズ学習

音楽音響信号が高々有限個の「部品」から構成されていると仮定し、音楽音響信号の構造を教師なし学習

  • 何を部品とみなすかによって異なる確率モデルが定式化 → 部品の個数が未知であるのでノンパラメトリックベイズモデル ＋ 変分ベイズ法などの最適化技法
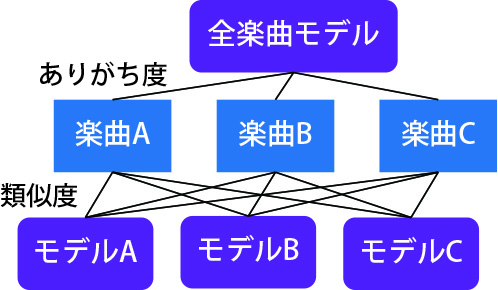
非負値行列分解
(Nonnegative Matrix Factorization: NMF)

p28_hihuchigyouretsubunkai

無限複合自己回帰モデル
(Infinite Composite Autoregressive Model: iCAR)

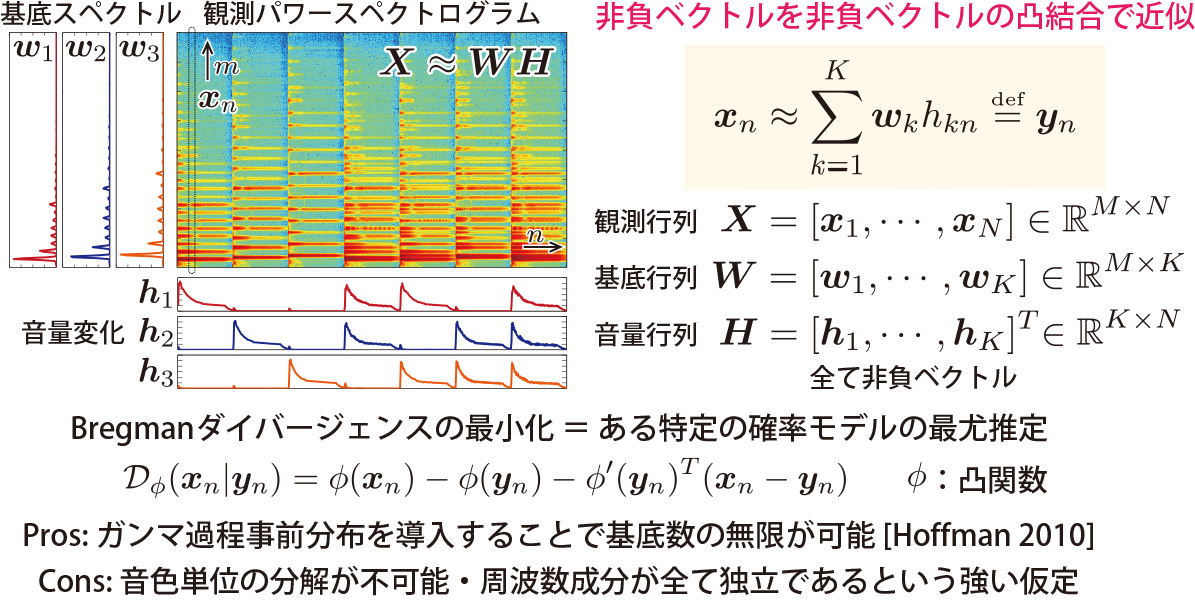
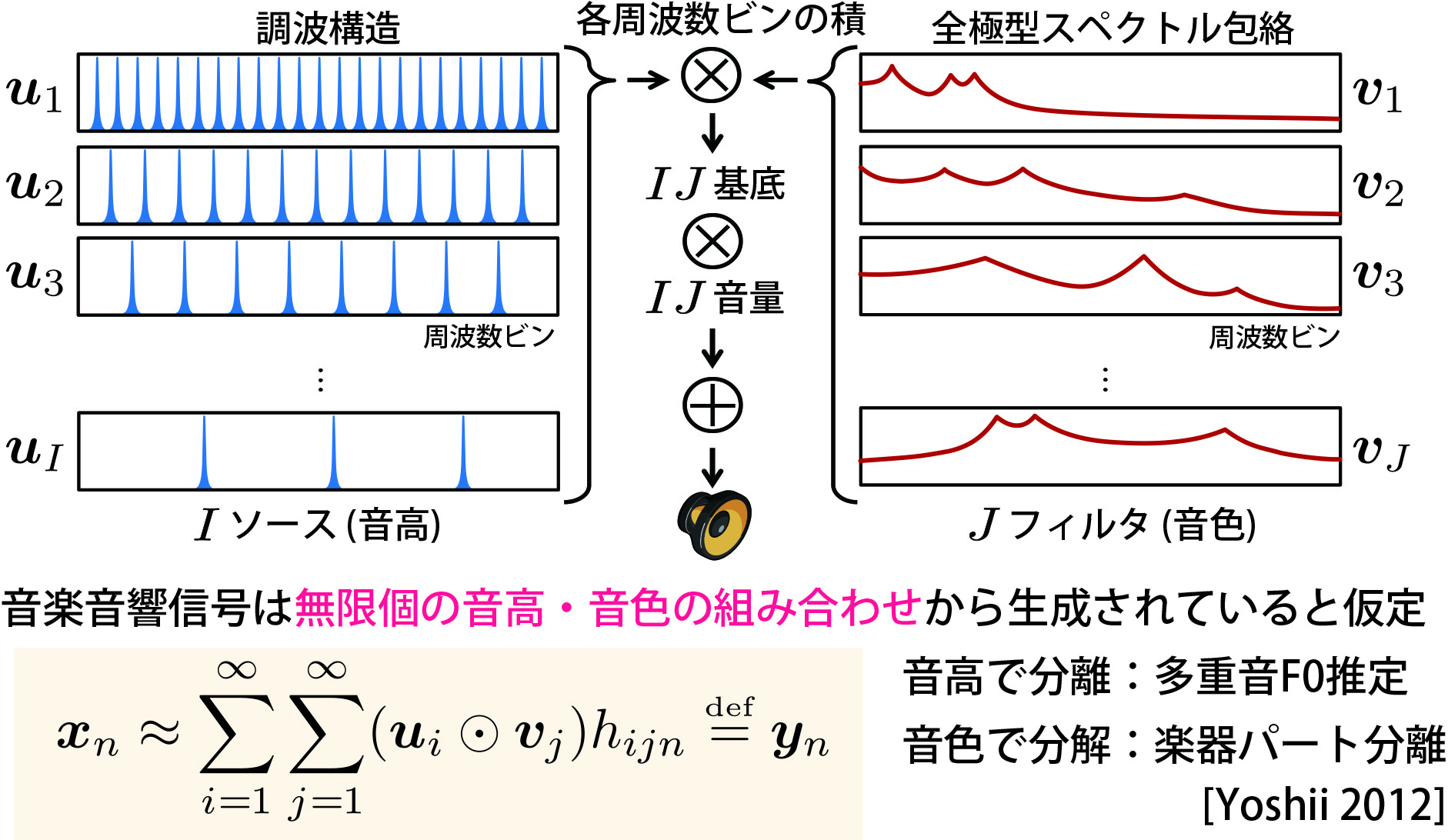
p28_mugenhukugoujikokaikimodel

無限半正定値テンソル分解
(Infinite Positive Semidefinite Tensor Factorization: iPSDTF)

p28_mugenhanseiteichi

楽譜情報に対するノンパラメトリックベイズ学習

重要な記号データのひとつであるコード系列に着目し、その背後にあるコード進行の確率モデルを教師なし学習

  • N-gramモデルにおけるNの値が可変・コードの語彙を恣意的に決めたくない
  • → ノンパラメトリックベイズモデル ＋ マルコフ連鎖モンテカルロ法などの最適化技法
語彙フリー無限グラムモデル
(Vocabulary-Free Infinity-gram Model)
  • 各コードについて最適なＮを推定可能 → コードパターンの発見[Yoshii 2011]
    理論上は無限語彙を扱うことが可能であるので将来的に新しいコードラベルが追加されても影響を受けない

p28_goifree